Finding Input Values to Matrix When You Know the Product

Today, permit's take a expect at everyone's favorite matrix application trouble, Leontief input-output models. You might know them simply as "technology matrix" problems, only actually the technology matrix is only one part of the trouble. The really interesting part is in the derivation of the matrix equation - something that most finite math courses seem to gloss over in the finish-of-semester frenzy.

So, let'due south take a look at a typical "technology matrix" problem, and see if we tin't sympathize how the problem actually works. Hopefully, it volition arrive easier to remember than an arbitrary formula.

Example: An economic system consists of two codependent industries - steel and lumber. It takes 0.1 units of steel and 0.5 units of lumber to make each unit of steel. It takes 0.ii units of steel and 0.0 units of lumber to brand each unit of lumber. The economic system volition consign \(sixteen\) units of steel and 8 units of lumber side by side month. How many units of steel and lumber will they need to product to meet this external need?

The crucial thing to sympathize about these problems is that both industries need some of each product (peradventure including their own) to brand more of that product. It's the old "you gotta spend coin to make coin" routine. So, in order to brand steel, the steel constitute needs a little bit of steel (hopefully less than it is producing), forth with some lumber. The lumberyard also needs some steel and lumber to make more lumber. This might be particularly relatable if yous've ever played a game that involves gathering and spending resources, like Age of Empires or Settlers of Catan.

The next thing to understand is that the problem is asking us for how much of each resource we need to produce - which will exist more than the amount we're exporting. Why? Because some of the steel and lumber we produce goes back into the ii industries to meet the production (which itself requires some steel and lumber, and and then on).

For both resources, the production can be cleaved into three parts:

1. The amount of the same resource needed to produce more of the resources;
2. The amount of the other resource needed to produce more of the resource;
3. The corporeality of the resources we need to have left over to export.

In the case of our steel-and-lumber operation, we can write two equations:

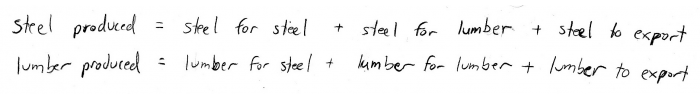
Next, let's try to write these equations more than mathematically. The trouble tells united states of america to define \(ten\) and \(y\) such that:

Now, let's effigy out expressions for the total steel needed for product of more than steel and lumber. These are going to depend on \(x\) and \(y\), since \(x\) and \(y\) represent the amount of steel and lumber we're producing. Well, the problem tells us that it takes 0.1 units of steel for each unit of steel, and 0.2 units of steel for each unit of measurement of lumber:

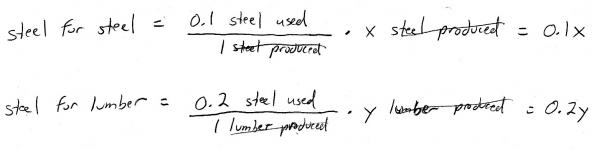
So notice that by dimensional analysis, both of these terms are referring to an amount of steel.

Nosotros tin can utilize the aforementioned idea process to find the amounts of lumber needed for producing steel and lumber:

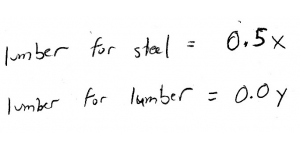
Substituting these expressions, forth with the external demands, into our overall production equations, we become:

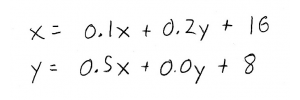
Notice that the first equation says that the total amount of steel we need to produce \((x)\) depends on itself \((0.1x)\), besides as the total amount of lumber we demand to produce \((0.2y)\) and the amount we need to export (\(16)\).

Great, nosotros've turned our problem into math! But, how exercise we solve information technology? Well, these are matrix awarding problems, subsequently all. So let's rewrite this system of equations every bit a matrix equation:

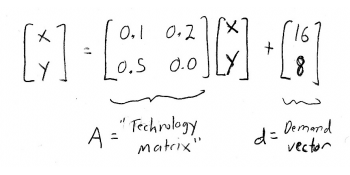
Matrix \(A\) is now our infamous "technology matrix", and the vector \(d\) is the demand vector. We tin likewise define a production vector:

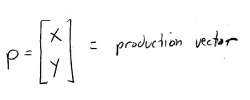
We can thus write our equation more compactly:

where our goal will be to solve for \(p\). How do we do this? Well, it'southward (virtually) like solving a regular, non-matrix equation - we need to group like terms.

The only question is, how do we group those like terms? Well normally, we'd factor out the \(p\) from both terms, and we'd have \((1-A)p\). The but problem is that we tin't subtract \(A\) (which is a matrix) from the number 1 (which is non a matrix). We need to use the "matrix equivalent" of the number 1 - the identity matrix!

With the 2x2 identity matrix, nosotros can now write:

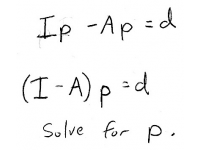
We already know \(A\), and so nosotros tin observe \((I-A)\) by subtracting the corresponding elements:

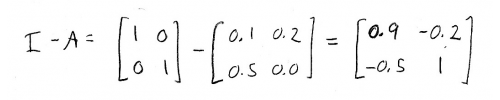
We also know \(d\), the demand vector, so we can set an augmented matrix that lets us solve for \(p\):

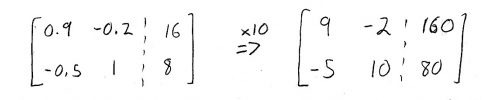
We'll multiply the whole thing by 10, to brand the arithmetic a little scrap easier. Now, nosotros tin can start performing row operations to solve the augmented matrix:

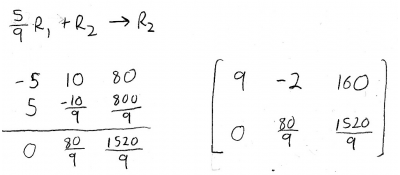
And finally,

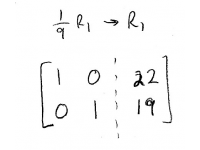
And then now, the right-hand column has the solution for \(p\)!

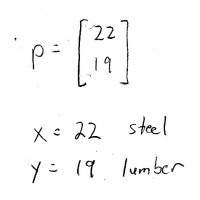
I hope this made sense, and skillful luck on finals!

christianlablen1983.blogspot.com

Source: https://bloomingtontutors.com/blog/how-to-understand-and-solve-leontief-input-output-model-technology-matrix-problems

Share this post